此文深入剖析困扰哥已久的浮点数表示和运算。

定义

Java 浮点数定义采纳 IEEE Standard 754 标准：单精度 float 32 位，双精度 double 64 位。本文主要以 float 为例。

最高位符号位
- 0 正 1 负
接 8 位指数位，并有 127 的偏移量
- 所以指数范围为：0 - 127 ~ (2⁸ - 1) - 127
- 全 0 和全 1 保留用特殊表示，所以指数域的修正范围为 -126 ~ 127
剩下 23 位为尾数域
- IEEE 要求浮点数必须是规范的，即小数点的左侧必须为1，这样腾出了一个二进制位来保存更多的尾数，即我们用 23 位尾数域表达了 24 位的尾数
- 所以尾数域上限为 2²⁴ - 1，即 0 ~ 16777215
- 10⁷ < 16777215 < 10⁸，所以 float 可以精确到小数点后 7 位（存疑）

特殊表示
- 指数全为 0，尾数为 0 时，表示 0
- 指数全为 1，尾数为 0 时，表示无穷大
- 指数全为 1，尾数不为 0 时，表示 NaN

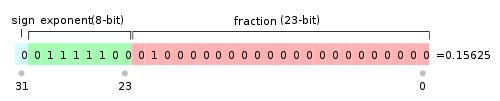
示例图中的数字表示解析：

符号位 0 ，表示正数
指数位 01111100 ，表示 2⁶ + 2⁵ + 2⁴ + 2³ + 2² - 127 = -3
尾数域左侧补 1 位，表示 101
最后值为 1 * 2^-3 + 1 * 2^-5 = 0.15625

精度

public static void main(String[] args) {
    float c = 1.0009765625F;
    System.out.println(Integer.toBinaryString(Float.floatToIntBits(c)));
    System.out.println(c);
    System.out.println(String.format("%.11f", c));
}

输出：

111111100000000010000000000000
1.0009766
1.00097656250

示例中的 c 精确到小数点后 10 位，可以精确的由二进制表示：1.0009765625 = 2⁰ + 2^-10。

第一行输出为其二进制表示，进行验证
0 01111111 00000000010000000000000
- 指数：2⁷ - 1 - 127 = 0
- 尾数：1.0000000001 = 2⁰ + 2^-10

以上输出的第二行表示 Java 对 float 处理的默认精度为 7 位，但是这不表示它的存储就丢失了精度。输出的第三行加入了指定的精度，即得到了无精度损失的浮点数。

所以这里得到我的个人结论： float 的 7 位精度是规约，而不是表示结构的限制。

二进制表示方法

0.1 = 1.6 / 16

= 1 / 16 + 0.6 / 1

= 1 / 16 + 1.2 / 32

= 1 / 16 + 1 / 32 + 0.2 / 32

= 1 / 16 + 1 / 32 + 1.6 / 2⁸

= 1 / 2⁴ + 1 / 2⁵ + 1 / 2⁸ + 0.6 / 2⁸

= …

第 6 步又回到了第 2 步一样的分子 0.6 ，所以这是一个无限循环小数

0.1 = 0.00011001 00011001 00011001 00011001…

场景

Puzzle 2

public static void main(String args[]) {
    System.out.println(2.00 - 1.10);    // 0.8999999999999999
}

这个简单的算式得到的结果不是期望的 0.9 ，而是 0.8999999999999999 。因为 1.1 不能被精确的保存为 double 类型，而被保存为了最接近 1.1 的值，不幸的是，这个值与 2.0 做减法运算后得到的不是最接近 0.9 的 double 值，而是输出的这个奇葩数。

public static void main(String args[]) {
    System.out.println(new BigDecimal("2.00").subtract(new BigDecimal("1.10")));   // 0.90
}

秘籍：需要精确表示时，用 BigDecimal(String str) ，永远不要用浮点数做运算。

Puzzle 28: Looper

while (i == i + 1) {

      }

给 i 一个声明，使上面的语句进入无限循环状态。。

double i = 1.0 / 0.0;
// Better yet, you can take advantage of a constant that is provided for you by the standard libraries:
double i = Double.POSITIVE_INFINITY;
// In fact, any sufficiently large floating-point value will do; for example:
double i = 1.0e40;

无穷大不用说。因为浮点数不能精确保存值，当一个数很大时，它的后继邻接数 (ulp) 与其差值可以大于 1 。

The distance between adjacent floating-point values is called an ulp, which is an acronym for unit in the last place. In release 5.0, the Math.ulp method was introduced to calculate the ulp of a float or double value.

秘籍：不要用浮点数做循环索引。

Puzzle 87: Strained Relations

数学上对于 = 的定义满足相等关系 (equivalence relation) 的三个条件

自反性：x ~ x for all x.
对称性：if x ~ y, then y ~ x.
传递性：if x ~ y and y ~ z, then x ~ z.

那么 Java 中的 == 呢

public static void main(String[] args) throws Exception {
    // 自反性不满足
    System.out.println(Double.NaN == Double.NaN);   // false

    // 传递性不满足
    long x = Long.MAX_VALUE;
    double y = (double)Long.MAX_VALUE;
    long z = Long.MAX_VALUE - 1;
    System.out.print((x == y) + " ");   // Imprecise! true
    System.out.print((y == z) + " ");   // Imprecise! true
    System.out.println(x == z);         // Precise    false

    // 对称性满足
}

总结

注意浮点数的精度丢失以及类型转换，相对于 float ，优先用 double 。

Hedley

Stay Hungry, Stay Foolish.

扑朔迷离浮点运算

定义

精度

二进制表示方法

场景

Puzzle 2

Puzzle 28: Looper

Puzzle 87: Strained Relations

总结

引用